2.11 行列の和と差

定義 2.44 (行列の和と差) 行列と行列の和をとする．これを

$\displaystyle A+B=C\,$

(284)

と表記する．行列の和は型が

$\displaystyle A$

$\displaystyle =[a_{ij}]_{m\times n}\,,\qquad B=[b_{ij}]_{m\times n}\,,\qquad C=[c_{ij}]_{m\times n}$

(285)

のとき定義される．各成分は

$\displaystyle A+B$

$\displaystyle =[a_{ij}]+[b_{ij}]=[c_{ij}]\,,\qquad c_{ij}=a_{ij}+b_{ij}$

(286)

と定義される．行列の差は同様に

$\displaystyle A-B$

$\displaystyle =[a_{ij}]-[b_{ij}]=[c_{ij}]\,,\qquad c_{ij}=a_{ij}-b_{ij}$

(287)

と定義される．

例 2.45 (行列の和の計算例)

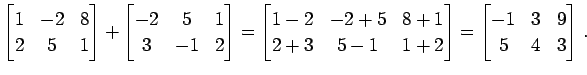$\displaystyle \begin{bmatrix}1 & -2 & 8 \\ 2 & 5 & 1 \end{bmatrix}+ \begin{bmat... ...-1 & 1+2 \end{bmatrix}= \begin{bmatrix}-1 & 3 & 9 \\ 5 & 4 & 3 \end{bmatrix}\,.$

(288)