2.8 行列のいろいろ 〜 エルミート行列，歪エルミート行列

定義 2.31 (エルミート行列) 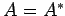  $A=A^{*}$ を満たす行列をエルミート行列（Hermite matrix）という．

例 2.32 (エルミート行列の具体例)  

$$A= \begin{bmatrix}1 & 1+i & -2-i \\ 1-i & 2 & 3+2i \\ -2+i & 3-2i & -3 \end{bmatrix}$$

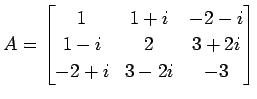問 2.33 (エルミート行列の成分)   エルミート行列の対角成分は実数となることを示せ．

定義 2.34 (歪エルミート行列) 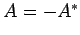  $A=-A^{*}$ を満たす行列を 歪エルミート行列（skew Hermite matrix）という．

例 2.35 (歪エルミート行列の具体例)  

$$A= \begin{bmatrix}i & 1+i & -2-i \\ -1+i & 2i & 3+2i \\ 2-i & -3+2i & -3i \end{bmatrix}$$

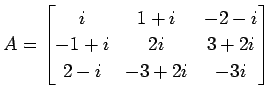問 2.36 (歪エルミート行列の成分)   歪エルミート行列の対角成分は純虚数となることを示せ．

Kondo Koichi
平成17年9月15日