3.5 積分の順番の入れ替え
例 3.31 (積分の順番の入れ替え)
領域 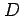 は
は  と
と 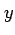 の両方に関して単純な領域であり,
の両方に関して単純な領域であり,
で与えられるとする.このとき,多重積分は
と書ける.![\includegraphics[width=0.4\textwidth]{sekibun-D1.eps}](img1412.png)
で与えられるとする.このとき,多重積分は
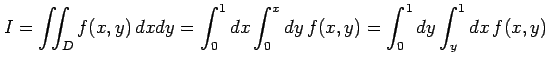 |
と書ける.
![\includegraphics[width=0.4\textwidth]{sekibun-D1.eps}](img1412.png)
例 3.32 (積分の順番の入れ替え)
領域 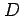 が
が  と
と  の両方に関して単純な領域であり,
の両方に関して単純な領域であり,
で与えられるとする.このとき,多重積分は
と書ける.![\includegraphics[width=0.4\textwidth]{sekibun-D5.eps}](img1415.png)
で与えられるとする.このとき,多重積分は
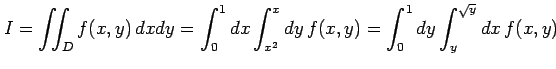 |
と書ける.
![\includegraphics[width=0.4\textwidth]{sekibun-D5.eps}](img1415.png)
例 3.33 (積分の順番の入れ替え)
領域
は に関して単純な領域である.
に関して単純な領域である.
 に関して単純な領域に書き換えると
に関して単純な領域に書き換えると
となる. このとき
が成り立つ.
は
となる. このとき
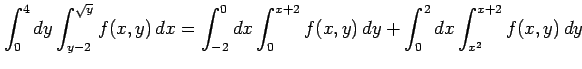 |
が成り立つ.
![\includegraphics[width=0.4\textwidth]{sekibun-D6.eps}](img1421.png) |
![\includegraphics[width=0.4\textwidth]{sekibun-D6x.eps}](img1422.png) |
|
(a) |
(b) |
Kondo Koichi

平成18年1月18日