5.11 解析関数
定義 5.19 (解析関数)
関数  がテイラー級数で表されるとき,
関数
がテイラー級数で表されるとき,
関数  は解析的(analytic)であるという.
解析的な関数を解析関数(analytic function)と呼ぶ.
は解析的(analytic)であるという.
解析的な関数を解析関数(analytic function)と呼ぶ.
定理 5.20 (解析関数の性質)
関数  ,
, 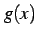 が解析的であるとき,次の関数
が解析的であるとき,次の関数
もまた解析的である.
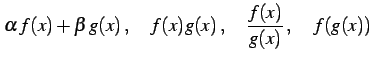 |
(666) |
もまた解析的である.
例 5.21 (テイラー級数の計算例)
関数
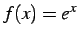 のテイラー級数は
のテイラー級数は
と表わされる. このとき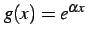 のテイラー級数を求める.
のテイラー級数を求める.
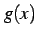 は
は  を用いると
を用いると
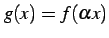 と書ける.
と書ける.
 のテイラー級数の
のテイラー級数の 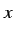 に
に 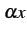 を代入すると
を代入すると
を得る. この展開式はテイラー級数の公式を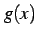 に適用したものと
同じものとなる.
同様に
に適用したものと
同じものとなる.
同様に
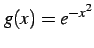 のテイラー級数は
のテイラー級数は
と求まる.
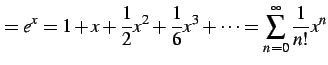 |
(667) |
と表わされる. このとき
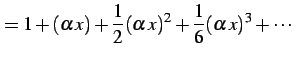 |
(668) | |
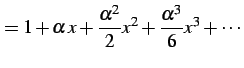 |
(669) |
を得る. この展開式はテイラー級数の公式を
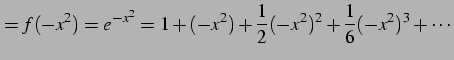 |
(670) | |
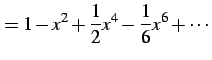 |
(671) | |
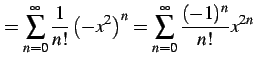 |
(672) |
と求まる.
Kondo Koichi

平成17年8月31日