1.5 上限，下限

次: 1.6 絶対値上: 1 数前: 1.4 区間

1.5 上限，下限

定義 1.11 (上限，下限) 集合 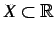$X\subset\mathbb{R}$ に対して
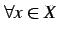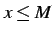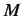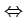
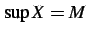
$\forall x\in X$ , $x\le M$ をみたす最小なが存在 $\Leftrightarrow$ $\sup X = M$
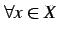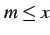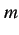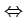
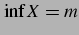
$\forall x\in X$ , $m \le x$ をみたす最大なが存在 $\Leftrightarrow$ $\inf X = m$
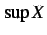$\sup X$ を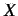の上限（supremum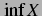）， $\inf X$ を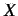の下限（infimum）という．

例 1.12 (上限，下限の具体例)

$\displaystyle \sup (1,2] = 2\,,$ $\displaystyle \inf (1,2] = 1$ (16)

$\displaystyle \sup \{x^2\,\vert\,-1\le x\le 1 \} = 1\,,$ $\displaystyle \inf \{x^2\,\vert\,-1\le x\le 1 \} = 0$ (17)

$\displaystyle \sup \{(-1)^{n}\,\vert\,n\in\mathbb{N} \} = 1\,,$ $\displaystyle \inf \{(-1)^{n}\,\vert\,n\in\mathbb{N} \} = -1$ (18)

Kondo Koichi
平成17年8月31日

$\displaystyle \sup (1,2] = 2\,,$	$\displaystyle \inf (1,2] = 1$	(16)
$\displaystyle \sup \{x^2\,\vert\,-1\le x\le 1 \} = 1\,,$	$\displaystyle \inf \{x^2\,\vert\,-1\le x\le 1 \} = 0$	(17)
$\displaystyle \sup \{(-1)^{n}\,\vert\,n\in\mathbb{N} \} = 1\,,$	$\displaystyle \inf \{(-1)^{n}\,\vert\,n\in\mathbb{N} \} = -1$	(18)