3.7 有理数巾の巾関数の微分
定理 3.17 (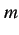 乗根関数の微分)
乗根関数の微分)
![$\displaystyle \frac{d}{dx}\,\sqrt[m]{x}= \frac{d}{dx}\,x^{\frac{1}{m}}= \frac{\sqrt[m]{x}}{m\,x}= \frac{1}{m}\,x^{\frac{1}{m}-1} \quad($](img675.png) |
(244) |
問 3.18
これを示せ.
である. ここで
であることを用いる.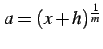 ,
,
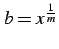 とおくと
とおくと
を得る.よって
となる.
(証明)
![]() とおく.
このとき
とおく.
このとき
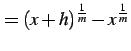 |
(245) |
である. ここで
| (246) | ||
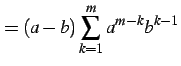 |
(247) | |
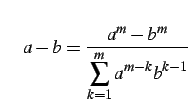 |
(248) |
であることを用いる.
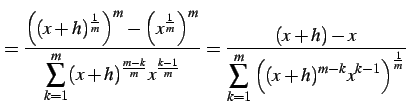 |
(249) | |
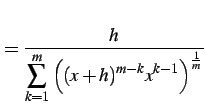 |
(250) |
を得る.よって
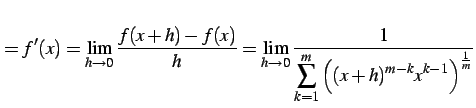 |
(251) | |
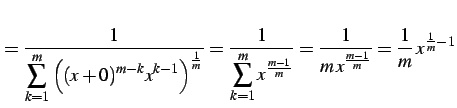 |
(252) |
となる.
Kondo Koichi

平成17年8月31日