3.5 自然数巾の巾関数の微分
定理 3.13 (巾関数の微分)
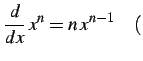 |
(231) |
問 3.14
これを示せ.
を得る.ここで
であることを用いると
となる.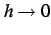 のとき
のとき
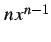 の項は生き残り,
その後ろの項は消える.
よって
の項は生き残り,
その後ろの項は消える.
よって
を得る.
(証明)
![]() とおき定義に従い計算すると,
とおき定義に従い計算すると,
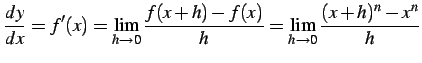 |
(232) |
を得る.ここで
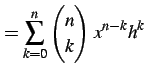 |
(233) | |
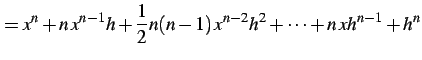 |
(234) | |
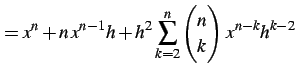 |
(235) |
であることを用いると
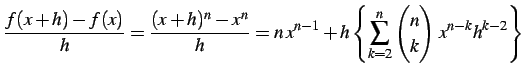 |
(236) |
となる.
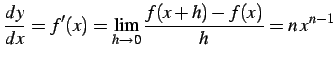 |
(237) |
を得る.
Kondo Koichi

平成17年8月31日