2.16 指数関数

指数関数（exponential function）は

$$y =a^{x}$$ (51)

により与えられる関数である． ただし，$a$ は定数である． 特に $a=e$ の場合が重要である． ここで $e$ は

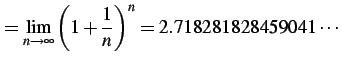$$e =\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^{n}=2.718281828459041\cdots$$ (52)

により定義されるネピア数と呼ばれる定数である． このとき

$$y=e^{x}=\exp(x)$$ (53)

と表される． 単に指数関数と呼ぶときはこの式を指す場合が多い．

定理 2.38 (指数関数の性質)   指数関数の次の性質をもつ：

(1)

$a^{x}a^{y}=a^{x+y}$.

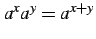(2)

$(a^x)^y=a^{xy}$.

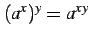(3)

$${\frac{a^{x}}{a^{y}}=a^{x-y}}$$.

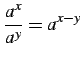(4)

$${\left(\frac{a}{b}\right)^x=\frac{a^x}{b^x}}$$.

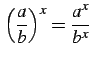問 2.39 (指数関数のグラフ)   指数関数のグラフを書け．

Kondo Koichi
平成17年8月31日