Next: 8 線形変換 Up: 2 線形写像 Previous: 6 線形写像の行列表示 Contents
7 線形写像の表現行列
定義 2.31 (線形写像の表現行列)
ベクトル空間 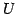 の基底を
の基底を
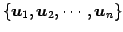 とし,
ベクトル空間
とし,
ベクトル空間 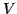 の基底を
の基底を
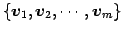 とする.
このとき,
線形写像
とする.
このとき,
線形写像  が
が
をみたすとき, 行列 を
を 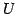 の基底
の基底
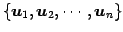 と
と
 の基底
の基底
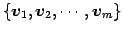 に関する
表現行列という.
に関する
表現行列という.
をみたすとき, 行列
注意 2.32 (表現行列)
前節の表現行列の定義では,
線形写像
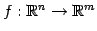 が
が
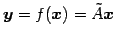 と表されるとき
と表されるとき
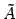 を表現行列と呼ぶ,というものであった.
この行列
を表現行列と呼ぶ,というものであった.
この行列 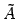 と本節の定義による表現行列
と本節の定義による表現行列  とは
基底を標準基底にとるとき一致する.
とは
基底を標準基底にとるとき一致する.
が成り立つ.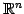 の任意のベクトル
の任意のベクトル
を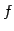 で写すと
で写すと
となる. と
と  は一致する.
は一致する.
線形写像
![]() を考える.
を考える.
![]() の標準基底を
の標準基底を
![]() とし,
とし,
![]() の標準基底を
の標準基底を
![]() とおく.
このとき,本節の表現行列の定義より
とおく.
このとき,本節の表現行列の定義より
が成り立つ.
を
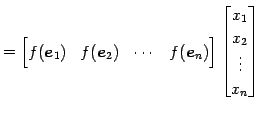 |
||
となる.
例 2.33 (表現行列の具体例)
線形写像
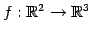 ;
;
を考える. 標準基底を
とする. このとき,
である.よって
が成立する. 線形写像 の標準基底における表現行列は
の標準基底における表現行列は  である.
である.
 |
を考える. 標準基底を
 |
とする. このとき,
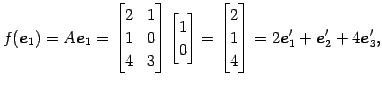 |
||
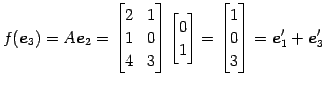 |
である.よって
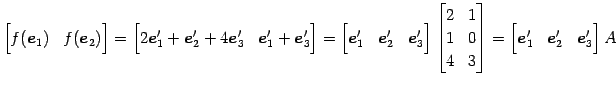 |
が成立する. 線形写像
注意 2.34 (表現行列)
線形写像
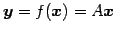 の標準基底に
おける表現行列は
の標準基底に
おける表現行列は 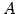 である.
である.
定理 2.35 (基底を取り換えたときの表現行列)
線形写像  の
の
 の基底
の基底
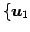 ,
,
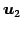 ,
,  ,
,
 と
と
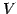 の基底
の基底
 ,
,
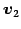 ,
,  ,
,
 に
関する表現行列を
に
関する表現行列を 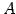 とする.
すなわち,
とする.
すなわち,
とする.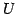 の基底
の基底
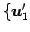 ,
,
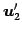 ,
, 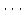 ,
,
 と
と
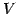 の基底
の基底
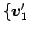 ,
,
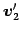 ,
, 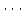 ,
,
 に
関する表現行列を
に
関する表現行列を 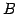 とする.
すなわち,
とする.
すなわち,
とする. このとき
が成り立つ. ここで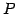 ,
,  は基底の変換行列であり,
は基底の変換行列であり,
である.
また,
よって,
が成り立つ.
とする.
とする. このとき
が成り立つ. ここで
である.
(証明)
また,
よって,
が成り立つ.
例 2.36 (基底を取り換えたときの表現行列の具体例)
線形写像
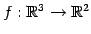 ;
;
を考える.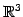 の基底を
の基底を
とし,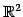 の基底を
の基底を
とする.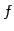 の基底
の基底
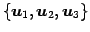 と
基底
と
基底
 に関する
表現行列
に関する
表現行列  を求める.
なすわち,
を求める.
なすわち,
をみたす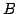 を求める.
まず,
を求める.
まず,
 の
標準基底
の
標準基底
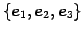 と
と
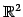 の
標準基底
の
標準基底
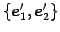 を考える.
このとき,標準基底における
を考える.
このとき,標準基底における 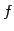 の表現行列は
の表現行列は 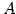 であるから,
であるから,
が成り立つ. つぎに,基底の変換行列は
である. 以上より,
が成り立つ. よって,
を得る.
 |
を考える.
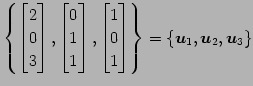 |
とし,
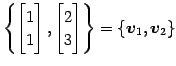 |
とする.
をみたす
が成り立つ. つぎに,基底の変換行列は
である. 以上より,
が成り立つ. よって,
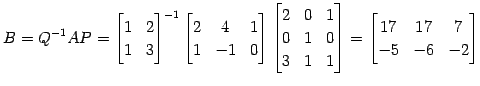 |
を得る.
Next: 8 線形変換 Up: 2 線形写像 Previous: 6 線形写像の行列表示 Contents
Kondo Koichi

Created at 2004/12/13