Next: 2 合成写像 Up: 2 線形写像 Previous: 2 線形写像 Contents
1 写像
定義 2.1 (写像)
集合 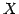 ,
, 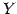 において,
において,
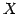 の各元
の各元 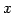 に対して
に対して 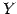 の元
の元 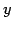 を 1 つずつ対応させる規則
を 1 つずつ対応させる規則 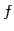 が
定まっているとき,
が
定まっているとき,
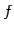 を
を 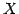 から
から 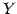 への写像(mapping)という.
これを
への写像(mapping)という.
これを
と表記する.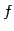 は関数(function)とも呼ばれる.
また,
は関数(function)とも呼ばれる.
また,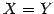 のときは,
特に写像のことを変換(transformation)ともいう.
のときは,
特に写像のことを変換(transformation)ともいう.
と表記する.
例 2.2 (写像の具体例)
ひらがなの集合とカタカナの集合
を考える. ひらがなをカタカナに書き換えるという規則を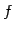 とするとき,
とするとき,
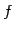 は
は 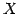 から
から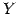 への写像であり,
への写像であり,
と書ける.
を考える. ひらがなをカタカナに書き換えるという規則を
と書ける.
例 2.3 (写像の具体例)
ある実数を 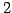 倍して 1 を足すという規則を
倍して 1 を足すという規則を 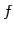 とする.
このとき
とする.
このとき 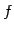 は写像であり,
は写像であり,
と表される.
と表される.
Next: 2 合成写像 Up: 2 線形写像 Previous: 2 線形写像 Contents
Kondo Koichi

Created at 2004/12/13