Next: 2 線形写像 Up: 1 ベクトル空間 Previous: 27 基底の変換 Contents
28 座標変換
定義 1.127 (座標)
ベクトル空間 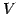 とその基底を
とその基底を
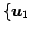 ,
,
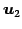 ,
, 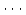 ,
,
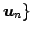 とする.
このとき
とする.
このとき 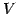 の任意の元
の任意の元 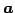 は
は
と表せる. 線形結合の係数の組
を基底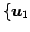 ,
,
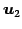 ,
, 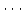 ,
,
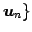 における座標(coordinate)という.
における座標(coordinate)という.
と表せる. 線形結合の係数の組
を基底
注意 1.128 (列行列の成分)
任意の列ベクトルは
と表させるので, 列ベクトルの成分の組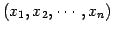 は
標準基底
は
標準基底
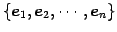 における
座標と見なされる.
における
座標と見なされる.
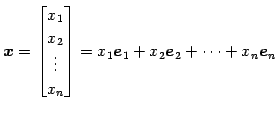 |
と表させるので, 列ベクトルの成分の組
ベクトル空間 ![]() の任意のベクトル
の任意のベクトル ![]() を考える.
基底
を考える.
基底
![]() ,
,
![]() ,
, ![]() ,
,
![]() のとき
のとき
とおく. 基底
とおく. これらくベクトルは等しいので,
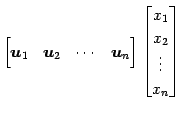 |
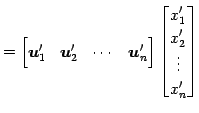 |
|
と表される. ここで, 基底
が成り立つので,
を得る. これより,
が成り立つ.
定義 1.129 (座標変換)
ベクトル 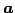 の
基底
の
基底
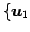 ,
,
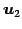 ,
, 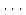 ,
,
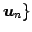 に
おける座標を
に
おける座標を 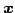 とし,
基底
とし,
基底
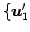 ,
,
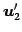 ,
, 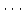 ,
,
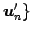 に
おける座標を
に
おける座標を 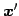 とする.
このとき
とする.
このとき
を座標変換(coordinate transform)という. ここで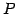 は
基底
は
基底
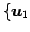 ,
,
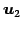 ,
, 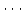 ,
,
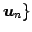 に
対する
基底
に
対する
基底
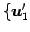 ,
,
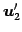 ,
, 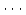 ,
,
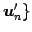 の
変換行列とする.
の
変換行列とする.
を座標変換(coordinate transform)という. ここで
例 1.130 (座標変換の具体例)
点
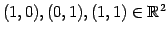 の
基底
の
基底
における座標を求める. 与えられた点は標準基底
における座標なので 基底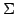 から基底
から基底 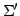 への座標変換を考える.
基底
への座標変換を考える.
基底 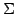 に対する基底
に対する基底 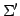 の変換行列を
の変換行列を 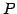 とおくと,
とおくと,
となる. このとき座標変換は
と表される. これを用いると
と表される. よって 座標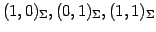 は
それぞれ
は
それぞれ
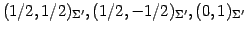 となる.
となる.
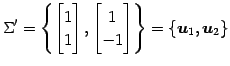 |
における座標を求める. 与えられた点は標準基底
における座標なので 基底
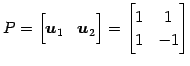 |
となる. このとき座標変換は
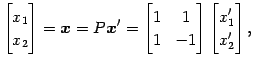 |
||
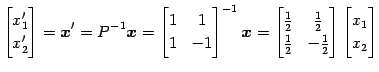 |
と表される. これを用いると
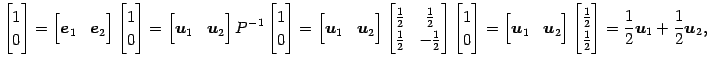 |
||
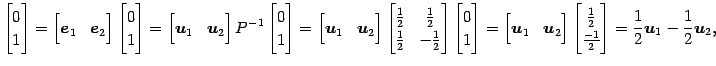 |
||
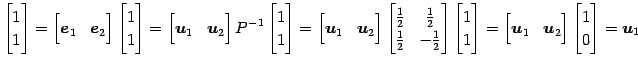 |
と表される. よって 座標
Next: 2 線形写像 Up: 1 ベクトル空間 Previous: 27 基底の変換 Contents
Kondo Koichi

Created at 2004/12/13