Next: 5 ベクトルの成分 Up: 1 ベクトルと図形 Previous: 3 ベクトルの演算 Contents
4 線形結合
定義 1.17 (線形結合)
ベクトル 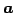 ,
, 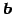 ,
,
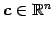 と
スカラー
と
スカラー 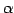 ,
,
 に対して,
に対して,
を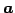 ,
, 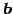 の
の
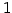 次結合または
線形結合(linear combination)という.
次結合または
線形結合(linear combination)という.
| (13) |
を
注意 1.18 (線形結合)
線形結合
 を考える.
を考える.
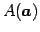 ,
,
 ,
,
 ,
,
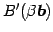 ,
,
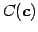 とする.
点
とする.
点 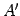 ,
,  はそれぞれ直線
はそれぞれ直線 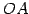 ,
,  の延長線上にあり,
の延長線上にあり,
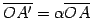 ,
,
 を満す.
点
を満す.
点 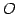 ,
, 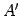 ,
, 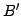 ,
,  は平行四辺形となる.
は平行四辺形となる.
例 1.19 (線形結合の具体例)
ベクトル
 を考える.
原点
を考える.
原点  から点
から点
 への延長線上の点で,
原点との長さが
への延長線上の点で,
原点との長さが
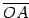 の
の  倍となる点を
倍となる点を 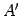 とする.
原点
とする.
原点 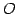 から点
から点
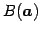 とは逆向きにのばした直線上の点で,
原点との長さが
とは逆向きにのばした直線上の点で,
原点との長さが
 の
の 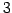 倍となる点を
倍となる点を  とする.
点
とする.
点  は線分
は線分 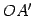 ,
,  からなる平行四辺形の
原点の対角線上の頂点となる.
からなる平行四辺形の
原点の対角線上の頂点となる.
定義 1.20 (基本ベクトル)
 空間の座標軸上の点
空間の座標軸上の点
の位置ベクトル
を の基本ベクトル(fundamental vectors)
という.
の基本ベクトル(fundamental vectors)
という.
| (14) |
の位置ベクトル
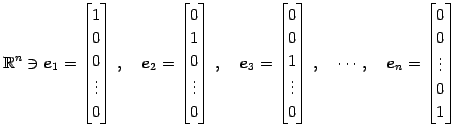 |
(15) |
を
例 1.21 (線形結合の具体例)
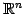 空間内の任意の点
空間内の任意の点 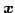 は
は
であり, ,
,
 ,
,  ,
,
 の
線形結合で表される.
の
線形結合で表される.
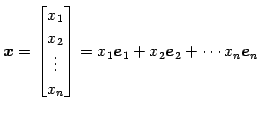 |
(16) |
であり,
Kondo Koichi

Created at 2004/11/26