9 行列の正則性と行列式

定理 4.66 (行列の正則性と行列式)   行列 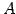$A$ が正則行列のとき 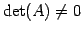$\det(A)\neq0$ が成り立つ．

問 4.67   これを示せ．

（証明） $A$ は逆行列をもつので，

$$AA^{-1}=A^{-1}A=E$$ (687)

が成立する． 各辺の行列式をとると

$$\det(AA^{-1})=\det(A)\det(A^{-1})\,,$$ (688)

$$\det(A^{-1}A)=\det(A^{-1})\det(A)=\det(A)\det(A^{-1})\,,$$ (689)

$$\det(E)=1$$ (690)

であるから

$$\det(A)\det(A^{-1})=1$$ (691)

を得る． よって

$$\det(A)\neq 0\,,\quad \det(A^{-1})\neq 0\,$$ (692)

が成り立つ．

定理 4.68 (逆行列の行列式)  

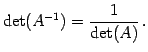$$\det(A^{-1})=\frac{1}{\det(A)}\,.$$ (693)

問 4.69 (逆行列の行列式)   これを示せ．

（証明） 前の定理の証明の $\det(A)\det(A^{-1})=1$ より示される．

Kondo Koichi
Created at 2004/11/26