Next: 14 点の直線への射影 Up: 1 ベクトルと図形 Previous: 12 内積と面積 Contents
13 直線の方程式
定義 1.51 (直線)
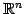 空間内の点
空間内の点 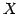 の位置ベクトルが
の位置ベクトルが
と表されるとき, 点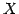 の軌跡を直線(line)という.
の軌跡を直線(line)という.
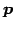 を方向ベクトル(tangent vector)という.
を方向ベクトル(tangent vector)という.
| (67) |
と表されるとき, 点
注意 1.52 (
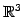 の直線の方程式)
直線
の直線の方程式)
直線
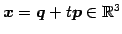 を考える.
ここで
を考える.
ここで
とおく.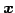 は点
は点
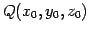 を通り
方向ベクトルが
を通り
方向ベクトルが 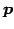 の直線である.
の直線である.
より,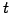 についてまとめると
直線の方程式は
についてまとめると
直線の方程式は
と表される. これは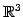 の直線の方程式
である.
の直線の方程式
である.
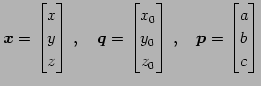 |
(68) |
とおく.
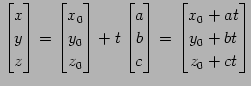 |
(69) |
より,
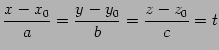 |
(70) |
と表される. これは
問 1.53 (
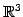 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 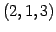 を通り
方向ベクトルが
を通り
方向ベクトルが
![$ {[-2\,\,3\,\,1]}^{T}$](img379.png) の
直線の方程式を求めよ.
の
直線の方程式を求めよ.
例 1.54 (
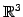 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 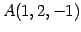 ,
,
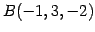 を通る直線の方程式を考える.
直線は点
を通る直線の方程式を考える.
直線は点 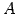 を通り,方向ベクトルは
を通り,方向ベクトルは
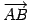 である.
すなわち,
である.
すなわち,
とおく. 直線の方程式のパラメータ表示は
である. を消去して
直線の方程式の成分表示は
を消去して
直線の方程式の成分表示は
である.
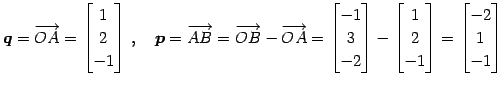 |
(71) |
とおく. 直線の方程式のパラメータ表示は
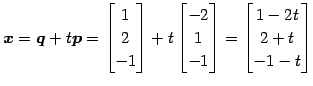 |
(72) |
である.
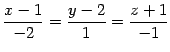 |
(73) |
である.
注意 1.55 (
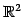 の直線の方程式)
直線
の直線の方程式)
直線
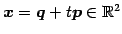 を考える.
このとき
を考える.
このとき
とおく.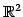 の直線の方程式は
の直線の方程式は
と表される. この式は 点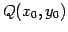 を通り
方向ベクトルが
を通り
方向ベクトルが
![$ \vec{p}={[a\,\,b]}^{T}$](img395.png) であることが
分かり易い形である.
であることが
分かり易い形である.
であり,または
となる. この式は![$ \vec{n}={[ a'\,\,\,\,b']}^{T}={[ b\,\,-a]}^{T}$](img401.png) を用いると
を用いると
とも表される.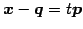 であるから,
ベクトル
であるから,
ベクトル 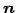 は
は
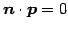 を満たす.
すなわち
を満たす.
すなわち 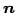 は方向ベクトル
は方向ベクトル 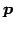 と直交する.
方向ベクトルと直交するベクトルを
法線ベクトル(normal vector)という.
と直交する.
方向ベクトルと直交するベクトルを
法線ベクトル(normal vector)という.
と表される. この式は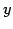 は
は 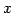 についての
についての 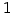 次関数であることと,
直線は点
次関数であることと,
直線は点
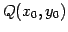 を通り
傾きが
を通り
傾きが 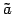 であることが分かり易い形である.
であることが分かり易い形である.
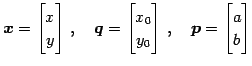 |
(74) |
とおく.
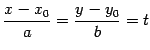 |
(75) |
と表される. この式は 点
式変形をする.
![]() ,
, ![]() ,
,
![]() とおく.
すると
とおく.
すると
| (76) |
であり,または
| (77) |
となる. この式は
| (78) |
とも表される.
さらに式変形する.
![]() とおく.
すると
とおく.
すると
| (79) |
と表される. この式は
問 1.56 (
 の直線の方程式)
点
の直線の方程式)
点 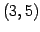 を通り方向ベクトルが
を通り方向ベクトルが
![$ {[2\,\,\,-1]}^{T}$](img417.png) の
直線の方程式を求めよ.
の
直線の方程式を求めよ.
問 1.57 (
 の直線の方程式)
点
の直線の方程式)
点 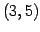 を通り法線ベクトルが
を通り法線ベクトルが
![$ {[2\,\,\,-1]}^{T}$](img420.png) の
直線の方程式を求めよ.
の
直線の方程式を求めよ.
問 1.58 (
 の直線の方程式の具体例)
点
の直線の方程式の具体例)
点 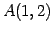 ,
, 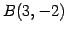 を通る直線の方程式を考える.
まず
を通る直線の方程式を考える.
まず
とおく.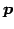 は方向ベクトルである.
直線の方程式のパラメータ表示は
は方向ベクトルである.
直線の方程式のパラメータ表示は
である.![$ \vec{x}={[x\,\,\,y]}^{T}$](img427.png) とおき
とおき 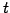 を消去すると,
直線の方程式の成分表示は
を消去すると,
直線の方程式の成分表示は
であり,変形して
である.法線ベクトルは![$ \vec{n}={[2\,\,\,1]}^{T}$](img431.png) である.
である.
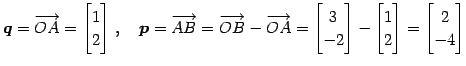 |
(80) |
とおく.
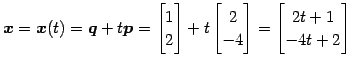 |
(81) |
である.
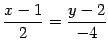 |
(82) |
であり,変形して
| (83) |
である.法線ベクトルは
定義 1.59 (単位方向ベクトル,単位法線ベクトル)
長さが 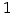 の方向ベクトルを
単位方向ベクトル(unit tangent vector)という.
長さが
の方向ベクトルを
単位方向ベクトル(unit tangent vector)という.
長さが 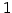 の法線ベクトルを
単位法線ベクトル(unit normal vector)という.
の法線ベクトルを
単位法線ベクトル(unit normal vector)という.
例 1.60
方程式
の単位方向ベクトルは
であり, 単位法線ベクトルは
である.
| (84) |
の単位方向ベクトルは
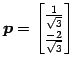 |
(85) |
であり, 単位法線ベクトルは
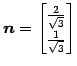 |
(86) |
である.
Next: 14 点の直線への射影 Up: 1 ベクトルと図形 Previous: 12 内積と面積 Contents
Kondo Koichi

Created at 2004/11/26