Next: 9 単位ベクトル Up: 1 ベクトルと図形 Previous: 7 内積 Contents
8 ノルム
定義 1.35 (ノルム)
ベクトル
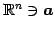 または
または
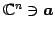 に対して
に対して
をベクトルのノルム(norm)または 長さ(length)という.
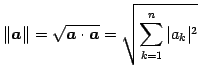 |
(41) |
をベクトルのノルム(norm)または 長さ(length)という.
例 1.36 (ノルムの具体例)
のノルムはそれぞれ
である.
のノルムはそれぞれ
である.
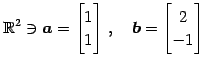 |
(42) |
のノルムはそれぞれ
| (43) | ||
| (44) |
である.
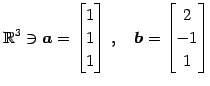 |
(45) |
のノルムはそれぞれ
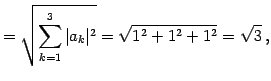 |
(46) | |
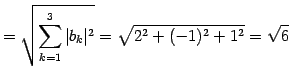 |
(47) |
である.
定理 1.37 (ノルムの性質)
シュバルツの不等式(Schwartz' inequality):
三角不等式(triangle inequality???):
| (48) |
三角不等式(triangle inequality???):
| (49) |
Next: 9 単位ベクトル Up: 1 ベクトルと図形 Previous: 7 内積 Contents
Kondo Koichi

Created at 2004/11/26