Next: 2 関数 Up: 1 数 Previous: 5 上限,下限 Contents
6 絶対値
定義 1.13 (絶対値)
実数 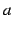 の絶対値(absolute value)を
の絶対値(absolute value)を
と定義する.
![$\displaystyle = \left\{ \begin{array}{cc} a & (a>0)\\ [1em] 0 & (a=0)\\ [1em] -a & (a<0) \end{array} \right.$](img80.png) |
(17) |
と定義する.
問 1.14 (絶対値の別の定義)
関数 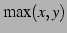 を
を
と定義するとき,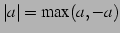 が成立することを示せ.
が成立することを示せ.
![$\displaystyle = \left\{ \begin{array}{ll} x & (x>y) \\ [1em] x & (x=y) \\ [1em] y & (x<y) \end{array} \right.$](img83.png) |
(18) |
と定義するとき,
定理 1.15 (絶対値の性質)
絶対値に関して次の性質が成り立つ:
- (1)
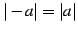 .
.
- (2)
-
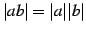 .
.
- (3)
-
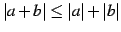 .
.
- (4)
-
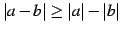 .
.
問 1.16 (絶対値の性質)
性質(1)-(4)を示せ.
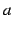 と
と 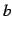 とをそれぞれ正,負,零の場合に分け,
全ての組合わせにおいて議論を行なう.
とをそれぞれ正,負,零の場合に分け,
全ての組合わせにおいて議論を行なう.
(証明)
Kondo Koichi

Created at 2004/08/14