Next: 6 数列の有界性と単調性 Up: 4 数列 Previous: 4 数列の極限に関する定理 Contents
5 収束する数列のいろいろ
例 4.17 (有理式で表される数列の極限)
一般項が
により与えられる数列を考える. 定理を適用して計算を試みる. 分子分母の極限をとり,
を得るがこれは誤りである. そもそも分子分母はそれぞれ発散するので定理は適用不可である. あらためて計算を行なう:
今回は有限確定となり極限が求まる. 計算の途中においては,定理が適用可能であるかの判断は難しい. 最終形まで計算した結果が有限確定または無限確定であれば, 途中の計算も定理が適用可能であることが多い.
で与えられる数列を考える.式を変形して極限を考える:
である数列の極限を考える. 式を変形して極限を考える:
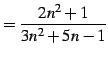 |
(399) |
により与えられる数列を考える. 定理を適用して計算を試みる. 分子分母の極限をとり,
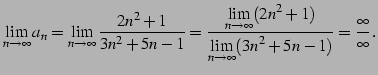 ←不確定 ←不確定 |
(400) |
を得るがこれは誤りである. そもそも分子分母はそれぞれ発散するので定理は適用不可である. あらためて計算を行なう:
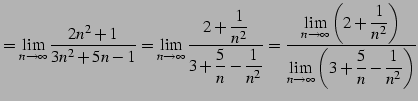 |
(401) | |
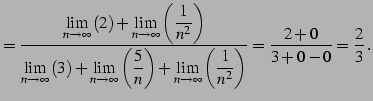 ←有限確定 ←有限確定 |
(402) |
今回は有限確定となり極限が求まる. 計算の途中においては,定理が適用可能であるかの判断は難しい. 最終形まで計算した結果が有限確定または無限確定であれば, 途中の計算も定理が適用可能であることが多い.
次に一般項が
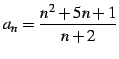 |
(403) |
で与えられる数列を考える.式を変形して極限を考える:
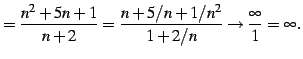 ←無限確定 ←無限確定 |
(404) |
最後に一般項が
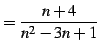 |
(405) |
である数列の極限を考える. 式を変形して極限を考える:
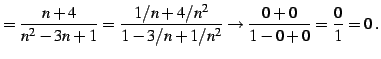 ←有限確定 ←有限確定 |
(406) |
以上をまとめると, 有理式で表される数列の極限は, 有理式の最大次数の巾で分子分母を割った後に極限をとればよい.
例 4.18 (根号を含む数列の極限)
一般項が
で与えられる数列の極限を考える. 式を次のように変形した後に極限をとる:
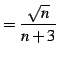 |
(407) |
で与えられる数列の極限を考える. 式を次のように変形した後に極限をとる:
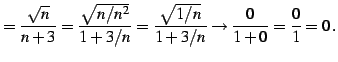 |
(408) |
問 4.19
参考書(p.12)第1章演習問題.
例 4.20 (等比数列の極限)
等比数列
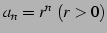 の極限を考える.
(i)
の極限を考える.
(i) 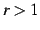 , (ii)
, (ii) 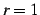 , (iii)
, (iii) 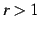 の場合に分けて議論する.
まず,(i)
の場合に分けて議論する.
まず,(i) 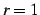 のとき,常に
のとき,常に 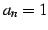 である.極限は
である.極限は 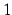 である.
つぎに,(iii)
である.
つぎに,(iii) 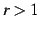 のとき,
のとき,
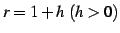 とおく.このとき
とおく.このとき 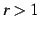 をみたす.
をみたす.
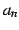 を
を 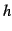 を用いて書き下すと
を用いて書き下すと
を得る.ここで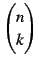 は
二項係数(binomial coefficient)であり,
は
二項係数(binomial coefficient)であり,
と定義する.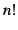 は階乗(fractorial number)であり,
は階乗(fractorial number)であり,
と再帰的に定義する.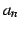 をあらためて書き直すと
をあらためて書き直すと
となる. 第三項以降を足したものは正となるので,
を得る.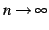 のとき
のとき
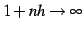 より
より
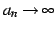 を得る.
最後に,(i)
を得る.
最後に,(i) 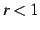 のときを考える.
のときを考える.
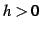 を用いて
を用いて 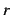 を
を
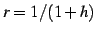 と置き換える.
このとき
と置き換える.
このとき 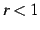 を満たす.
を満たす.
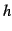 を用いて
を用いて 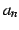 を書き下すと,
を書き下すと,
を得る. 不等式
が成立する.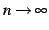 のとき
のとき
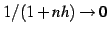 であるから,
はさみうちの定理より
であるから,
はさみうちの定理より
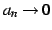 を得る.
以上をまとめると
を得る.
以上をまとめると
が求まる.
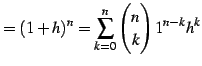 |
(409) |
を得る.ここで
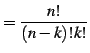 |
(410) |
と定義する.
| (411) |
と再帰的に定義する.
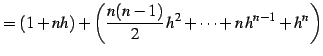 |
(412) |
となる. 第三項以降を足したものは正となるので,
| (413) |
を得る.
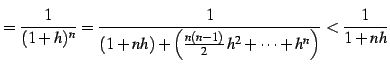 |
(414) |
を得る. 不等式
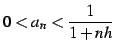 |
(415) |
が成立する.
![$\displaystyle \lim_{n\to\infty} a_{n}=\lim_{n\to\infty} r^{n}= \left\{ \begin{array}{cc} 0 & (r<1)\\ [1em] 1 & (r=1)\\ [1em] \infty & (r>1) \end{array} \right.$](img1405.png) |
(416) |
が求まる.
公式 4.21 (ネピア数)
この定数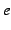 をネピア数(Napier's number)という.
をネピア数(Napier's number)という.
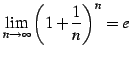 |
(417) |
この定数
問 4.22
極限
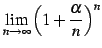
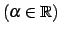 を求めよ.
を求めよ.
問 4.23
次の漸化式で与えられる数列の一般項と極限を求めよ.
(2)
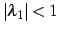 かつ
かつ
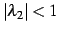 のとき
のとき 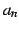 は 0 に収束する.
それ以外は発散する.
は 0 に収束する.
それ以外は発散する.
- (1)
-
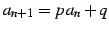 .
.
- (2)
-
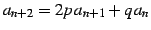 .
.
(答え) (1)
![$\displaystyle = \left\{\begin{array}{lc} \displaystyle{ p^{n-1}\left(a_{1}-\fra...
...ht)} & (p\neq1) \\ [1em] \displaystyle{(n-1)q+a_{1}} & (p=1) \end{array}\right.$](img1413.png) |
(418) |
![$\displaystyle \lim_{n\to\infty}a_{n}= \left\{ \begin{array}{lc} \infty & (\vert p\vert\geq1) \\ [1em] 0 & (\vert p\vert<1) \end{array} \right.$](img1414.png) |
(419) |
(2)
| (420) | ||
| (421) | ||
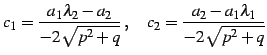 |
(422) |
Next: 6 数列の有界性と単調性 Up: 4 数列 Previous: 4 数列の極限に関する定理 Contents
Kondo Koichi

Created at 2004/08/14