Next: 8 三角関数の微分 Up: 3 微分法 Previous: 6 対数関数の微分 Contents
7 指数関数の微分
定理 3.22 (指数関数の微分)
関数 | (254) | ||
| (255) |
問 3.23
これを示せ.
である.これと逆関数の微分公式より
を得る.
(証明)
![]() とおく.
このとき逆関数とその微分は
とおく.
このとき逆関数とその微分は
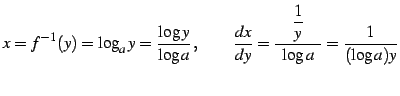 |
(256) |
である.これと逆関数の微分公式より
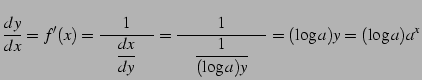 |
(257) |
を得る.
Kondo Koichi

Created at 2004/08/14