Next: 6 対数関数の微分 Up: 3 微分法 Previous: 4 定数の微分 Contents
5 巾関数の微分
定理 3.13 (巾関数の微分)
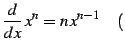 |
(223) |
問 3.14
これを示せ.
を得る.ここで
であることを用いると
となる.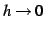 のとき
のとき
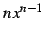 の項は生き残り,
その後ろの項は消える.
よって
の項は生き残り,
その後ろの項は消える.
よって
を得る.
(証明)
![]() とおき定義に従い計算すると,
とおき定義に従い計算すると,
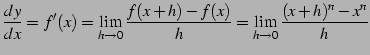 |
(224) |
を得る.ここで
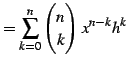 |
(225) | |
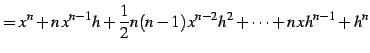 |
(226) | |
 |
(227) |
であることを用いると
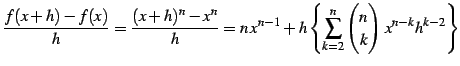 |
(228) |
となる.
 |
(229) |
を得る.
定理 3.15 (負巾関数の微分)
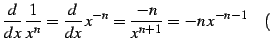 |
(230) |
問 3.16
これを示せ.
となる.これを用いて
を得る.
(証明)
![]() とおく.
このとき
とおく.
このとき
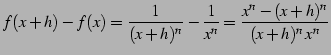 |
(231) | |
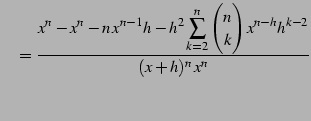 |
(232) | |
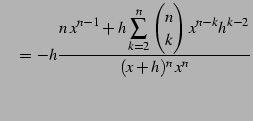 |
(233) |
となる.これを用いて
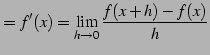 |
(234) | |
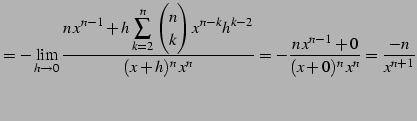 |
(235) |
を得る.
定理 3.17 (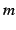 乗根関数の微分)
乗根関数の微分)
![$\displaystyle \frac{d}{dx}\,\sqrt[m]{x}= \frac{d}{dx}\,x^{\frac{1}{m}}= \frac{\sqrt[m]{x}}{m\,x}= \frac{1}{m}\,x^{\frac{1}{m}-1} \quad($](img872.png) |
(236) |
問 3.18
これを示せ.
である. ここで
であることを用いる.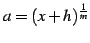 ,
,
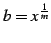 とおくと
とおくと
を得る.よって
となる.
(証明)
![]() とおく.
このとき
とおく.
このとき
| (237) |
である. ここで
| (238) | ||
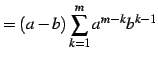 |
(239) | |
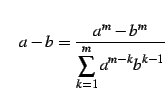 |
(240) |
であることを用いる.
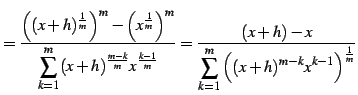 |
(241) | |
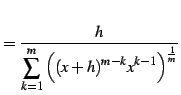 |
(242) |
を得る.よって
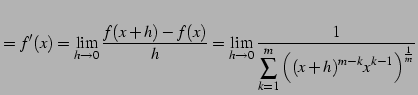 |
(243) | |
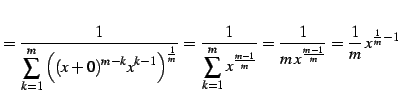 |
(244) |
となる.
定理 3.19 (巾関数の微分)
と表されるのでこれを微分すると
を得る.
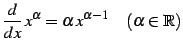 |
(245) |
(証明)
次節の
![]() ,
,
![]() が既に証明済みであるとする.
このとき
が既に証明済みであるとする.
このとき
| (246) |
と表されるのでこれを微分すると
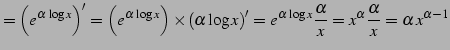 |
(247) |
を得る.
Next: 6 対数関数の微分 Up: 3 微分法 Previous: 4 定数の微分 Contents
Kondo Koichi

Created at 2004/08/14