Next: 2 導関数 Up: 3 微分法 Previous: 3 微分法 Contents
1 微分係数
定義 3.1 (微分と微分係数)
関数 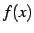 が
が 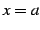 において連続で,極限
において連続で,極限
が存在するとき,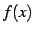 は
は 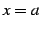 において微分可能(differentiable)
であるという.
このとき有限確定した極限を
において微分可能(differentiable)
であるという.
このとき有限確定した極限を 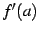 と表記し,
と表記し,
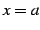 における
における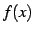 の
微分係数(differential coefficient)と呼ぶ.
の
微分係数(differential coefficient)と呼ぶ.
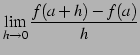 |
(180) |
が存在するとき,
定義 3.2 (右微分係数,左微分係数)
右極限による関数 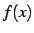 の微分係数を
の微分係数を
と書き,右微分係数(right differential coefficient)と呼ぶ. 左極限による関数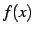 の微分係数を
の微分係数を
と書き,左微分係数(left differential coefficient)と呼ぶ.
 |
(181) |
と書き,右微分係数(right differential coefficient)と呼ぶ. 左極限による関数
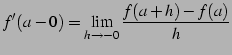 |
(182) |
と書き,左微分係数(left differential coefficient)と呼ぶ.
注意 3.3 (微分係数の存在)
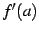 が存在するとは,すなわち
が存在するとは,すなわち 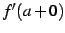 ,
, 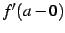 が存在し,
かつ
が存在し,
かつ
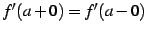 が成り立つことを意味する.
が成り立つことを意味する.
例 3.4 (微分係数の具体例)
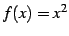 の
の 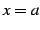 における微分係数を求める.まず
における微分係数を求める.まず
とおく. を計算すると
を計算すると
を得る.よって
により微分係数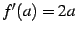 が求まる.
が求まる.
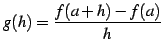 |
(183) |
とおく.
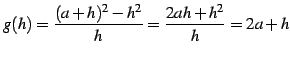 |
(184) |
を得る.よって
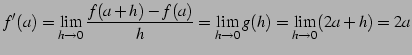 |
(185) |
により微分係数
例 3.5 (微分不可能な点の具体例)
関数 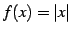 は
は 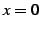 において連続であるが,微分可能ではない.
以下これを示す.まず
において連続であるが,微分可能ではない.
以下これを示す.まず
とおく.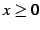 ,
, 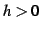 のとき
のとき
である.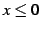 ,
, 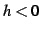 のとき
のとき
となる.これより
を得る.右微分係数と左微分係数は存在するがその値は異なる. よって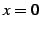 における微分係数
における微分係数 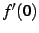 は存在しない.
は存在しない.
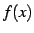 は
は 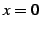 において微分不可能である.
において微分不可能である.
 |
(186) |
とおく.
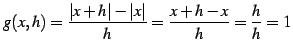 |
(187) |
である.
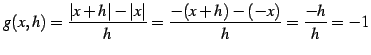 |
(188) |
となる.これより
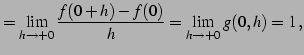 |
(189) | |
 |
(190) |
を得る.右微分係数と左微分係数は存在するがその値は異なる. よって
Next: 2 導関数 Up: 3 微分法 Previous: 3 微分法 Contents
Kondo Koichi

Created at 2004/08/14