Next: 17 連続と不連続 Up: 2 関数 Previous: 15 逆双曲線関数 Contents
16 関数の極限
定義 2.51 (右極限,左極限)
変数 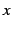 を右から
を右から 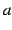 に近づけたときの
に近づけたときの 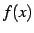 の値が
の値が 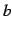 に近づくとき
に近づくとき
と書き,右極限(right-hand limit)と呼ぶ. 同様に, 変数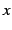 を左から
を左から 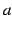 に近づけたときの
に近づけたときの 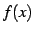 の値が
の値が 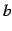 に近づくとき
に近づくとき
と書き,左極限(left-hand limit)と呼ぶ.
と書くこともある.
| (108) |
と書き,右極限(right-hand limit)と呼ぶ. 同様に, 変数
| (109) |
と書き,左極限(left-hand limit)と呼ぶ.
また略記として
| (110) |
と書くこともある.
定義 2.52 (関数の極限)
変数 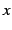 を
を 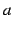 に近づけるとき,
その近づけ方に依らず全て同じ極限となるとき,
すなわち
に近づけるとき,
その近づけ方に依らず全て同じ極限となるとき,
すなわち
が成り立つとき, そのときに限り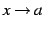 における関数
における関数 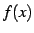 の極限が存在し,
の極限が存在し,
と書く. 極限が存在するとき次のように表現する:
収束しないとき発散する(divergent)という.
| (111) |
が成り立つとき, そのときに限り
と書く. 極限が存在するとき次のように表現する:
| 関数 |
(113) | |
| (114) | ||
| (115) | ||
| (116) |
収束しないとき発散する(divergent)という.
例 2.53 (関数の極限の具体例)
関数 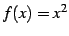 を考える.
このとき
を考える.
このとき
となる. 右からの極限も左からの極限も存在し同じ値となる. よって
である.
| (117) |
となる. 右からの極限も左からの極限も存在し同じ値となる. よって
| (118) |
である.
例 2.54 (関数の極限の具体例)
関数
を考える.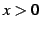 のとき
のとき
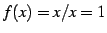 であるから
右極限は
であるから
右極限は
となる.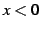 のとき
のとき
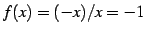 であるから
左極限は
であるから
左極限は
となる. 右極限と左極限が一致しないので, 極限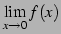 は存在しない.
は存在しない.
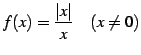 |
(119) |
を考える.
| (120) |
となる.
| (121) |
となる. 右極限と左極限が一致しないので, 極限
例 2.55 (関数の極限の具体例)
関数
を考える.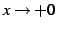 のとき
のとき
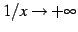 である.
である.
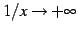 であるから
であるから 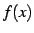 は
は 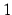 と
と 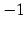 の間を振動する.
よって右極限
の間を振動する.
よって右極限
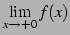 は存在しない.
は存在しない.
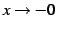 のとき
のとき
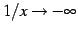 である.
以下同様で左極限
である.
以下同様で左極限
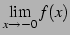 は存在しない.
右極限も左極限も存在しないので,
極限
は存在しない.
右極限も左極限も存在しないので,
極限
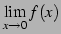 は存在しない.
は存在しない.
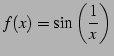 |
(122) |
を考える.
定理 2.56 (関数の極限に関する性質)
関数 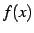 ,
, 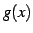 に関して極限
に関して極限
が存在するならば,
が成り立つ. ただし,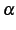 ,
, 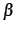 は定数である.
は定数である.
| (123) |
が存在するならば,
| (124) | ||
| (125) | ||
| (126) | ||
| (127) | ||
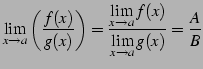 |
(128) |
が成り立つ. ただし,
例 2.57 (関数の極限の計算例)
| (129) | ||
| (130) | ||
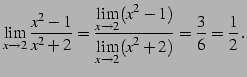 |
(131) |
変数 ![]() の値が正で限りなく大きくなるとき
の値が正で限りなく大きくなるとき
![]() と書く.
変数
と書く.
変数 ![]() の値が負で限りなく小さくなるとき
の値が負で限りなく小さくなるとき
![]() と書く.
また,
変数
と書く.
また,
変数 ![]() の値が正で限りなく大きくなるとき
の値が正で限りなく大きくなるとき
![]() と書く.
変数
と書く.
変数 ![]() の値が負で限りなく小さくなるとき
の値が負で限りなく小さくなるとき
![]() と書く.
と書く.
例 2.58 (関数の極限の計算例)
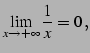 |
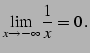 |
(132) | ||
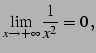 |
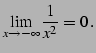 |
(133) | ||
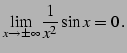 |
(134) | |||
| (135) | ||||
| (136) | ||||
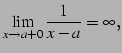 |
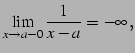 |
(137) | ||
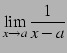 :存在ない :存在ない |
(138) | |||
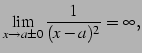 |
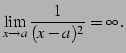 |
(139) | ||
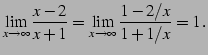 |
(140) | |||
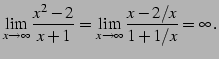 |
(141) |
公式 2.59 (ネピア数)
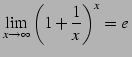 |
(142) |
公式 2.60
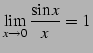 |
(143) |
問 2.61
参考書(p.31)問題 2-3.
問 2.62 (関数の極限の計算)
| (144) | ||
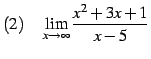 |
(145) | |
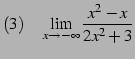 |
(146) | |
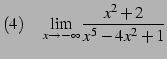 |
(147) | |
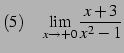 |
(148) | |
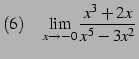 |
(149) | |
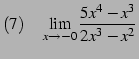 |
(150) | |
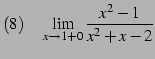 |
(151) | |
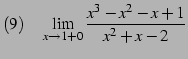 |
(152) | |
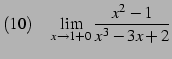 |
(153) | |
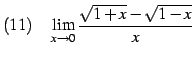 |
(154) | |
| (155) | ||
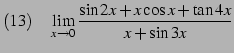 |
(156) | |
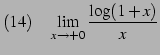 |
(157) | |
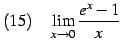 |
(158) | |
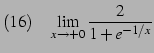 |
(159) | |
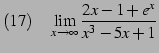 |
(160) | |
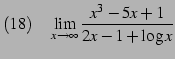 |
(161) | |
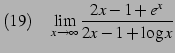 |
(162) |
Next: 17 連続と不連続 Up: 2 関数 Previous: 15 逆双曲線関数 Contents
Kondo Koichi

Created at 2004/08/14