Next: 18 コーシーの主値積分 Up: 5 積分法 Previous: 16 回転体の体積 Contents
17 広義積分
有限区間で連続な関数に対し定義される量が定積分である. 不連続点を含む区間や無限区間における積分へ拡張する. この拡張された積分を広義積分(improper integral)という.
定義 5.58 (不連続点を含む区間での広義積分)
関数 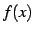 が
が 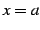 で不連続で,
で不連続で, ![$ (a,b]$](img2975.png) で連続なとき,
で連続なとき,
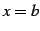 で不連続で,
で不連続で,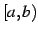 で連続なとき,
で連続なとき,
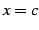
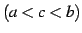 で不連続で,
で不連続で,![$ [a,b]$](img2982.png) で連続なとき,
で連続なとき,
以上の極限が存在するとき広義積分は収束するという.
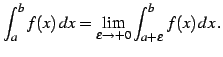 |
(1044) |
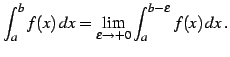 |
(1045) |
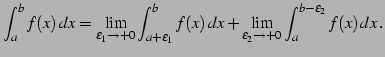 |
(1046) |
以上の極限が存在するとき広義積分は収束するという.
例 5.59 (不連続点を含む広義積分の具体例)
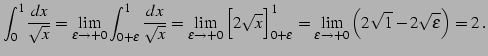 |
(1047) | |
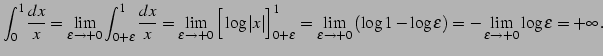 |
(1048) | |
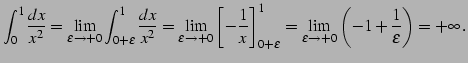 |
(1049) |
定理 5.60 (広義積分の収束次数)
実数 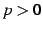 に対して次の広義積分が成り立つ:
に対して次の広義積分が成り立つ:
![$\displaystyle \int_{0}^{1}\frac{dx}{x^p}= \left\{\begin{array}{ll} \displaystyle{\frac{1}{1-p}} & (0<p<1) \\ [1em] +\infty & (p\geq1) \end{array}\right.$](img2988.png) |
(1050) |
問 5.61 (広義積分の収束次数)
これを示せ.
定義 5.62 (無限区間での広義積分)
関数 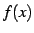 が無限区間
が無限区間
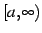 で連続なとき,
で連続なとき,
無限区間![$ (-\infty,b]$](img2992.png) で連続なとき,
で連続なとき,
無限区間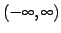 で連続なとき,
で連続なとき,
以上の極限が存在するとき広義積分は収束するという.
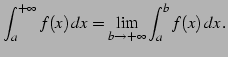 |
(1051) |
無限区間
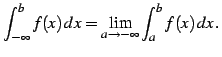 |
(1052) |
無限区間
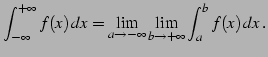 |
(1053) |
以上の極限が存在するとき広義積分は収束するという.
例 5.63 (無限区間での広義積分の具体例)
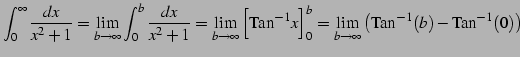 |
(1054) | |
| (1055) |
例 5.64 (無限区間での広義積分の具体例)
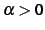 に対して
に対して
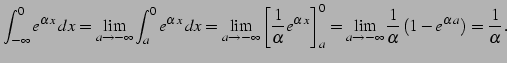 |
(1056) |
例 5.65 (無限区間での広義積分の具体例)
![$\displaystyle \int_{1}^{\infty}\frac{dx}{\sqrt{x}}= \lim_{b\to\infty} \int_{1}^...
...g[2\sqrt{x}\Big]_{1}^{b}= \lim_{b\to\infty} \left(2\sqrt{b}-2\right)=+\infty\,.$](img3000.png) |
(1057) | |
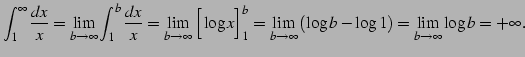 |
(1058) | |
![$\displaystyle \int_{1}^{\infty}\frac{dx}{x^2}= \lim_{b\to\infty} \int_{1}^{b}\f...
...-\frac{1}{x}\right]_{1}^{b}= \lim_{b\to\infty} \left(-\frac{1}{b}+1\right)=1\,.$](img3002.png) |
(1059) |
定理 5.66 (広義積分の収束次数)
実数 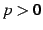 に対して次の広義積分が成り立つ:
に対して次の広義積分が成り立つ:
![$\displaystyle \int_{1}^{\infty}\frac{dx}{x^p}= \left\{\begin{array}{ll} +\infty & (0<p\leq1) \\ [1em] \displaystyle{\frac{1}{1-p}} & (p>1) \end{array}\right.$](img3004.png) |
(1060) |
問 5.67 (広義積分の収束次数)
これを示せ.
Next: 18 コーシーの主値積分 Up: 5 積分法 Previous: 16 回転体の体積 Contents
Kondo Koichi
Created at 2003/08/29