3 不定積分の基本的な計算

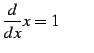$\displaystyle \frac{d}{dx}x=1 \qquad$	$\displaystyle \Leftrightarrow\qquad \int dx=x+C$	(785)
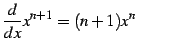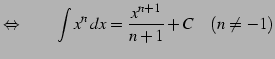$\displaystyle \frac{d}{dx}x^{n+1}=(n+1)x^{n} \qquad$	$\displaystyle \Leftrightarrow\qquad \int x^{n}\,dx=\frac{x^{n+1}}{n+1}+C \quad(n\neq-1)$	(786)
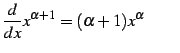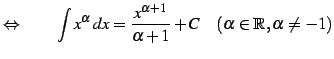$\displaystyle \frac{d}{dx}x^{\alpha+1}=(\alpha+1)x^{\alpha} \qquad$	$\displaystyle \Leftrightarrow\qquad \int x^{\alpha}\,dx=\frac{x^{\alpha+1}}{\alpha+1}+C \quad(\alpha\in\mathbb{R},\alpha\neq-1)$	(787)
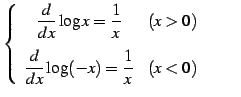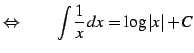$\displaystyle \left\{\begin{array}{cc} \displaystyle{\frac{d}{dx}\log x=\frac{1... ...isplaystyle{\frac{d}{dx}\log(-x)=\frac{1}{x}} & (x<0) \end{array}\right. \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{x}\,dx=\log\vert x\vert+C$	(788)
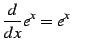$\displaystyle \frac{d}{dx}e^{x}=e^{x} \qquad$	$\displaystyle \Leftrightarrow\qquad \int e^{x}\,dx=e^{x}+C$	(789)
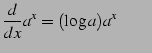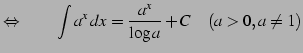$\displaystyle \frac{d}{dx}a^{x}=(\log a)a^{x} \qquad$	$\displaystyle \Leftrightarrow\qquad \int a^{x}\,dx=\frac{a^{x}}{\log a}+C \quad(a>0,a\neq1)$	(790)
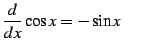$\displaystyle \frac{d}{dx}\cos x=-\sin x \qquad$	$\displaystyle \Leftrightarrow\qquad \int\sin x\,dx=-\cos x+C$	(791)
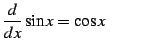$\displaystyle \frac{d}{dx}\sin x=\cos x \qquad$	$\displaystyle \Leftrightarrow\qquad \int\cos x\,dx=\sin x+C$	(792)
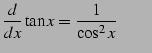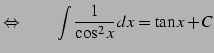$\displaystyle \frac{d}{dx}\tan x=\frac{1}{\cos^2x} \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{\cos^2 x}\,dx=\tan x+C$	(793)
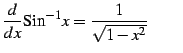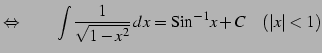$\displaystyle \frac{d}{dx}\mathrm{Sin}^{-1} x=\frac{1}{\sqrt{1-x^2}} \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{\sqrt{1-x^2}}\,dx=\mathrm{Sin}^{-1} x+C \quad(\vert x\vert<1)$	(794)
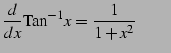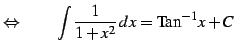$\displaystyle \frac{d}{dx}\mathrm{Tan}^{-1} x=\frac{1}{1+x^2} \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{1+x^2}\,dx=\mathrm{Tan}^{-1} x+C$	(795)
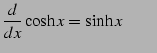$\displaystyle \frac{d}{dx}\cosh x=\sinh x \qquad$	$\displaystyle \Leftrightarrow\qquad \int\sinh x\,dx=\cosh x+C$	(796)
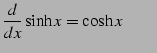$\displaystyle \frac{d}{dx}\sinh x=\cosh x \qquad$	$\displaystyle \Leftrightarrow\qquad \int\cosh x\,dx=\sinh x+C$	(797)
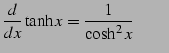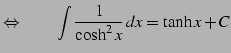$\displaystyle \frac{d}{dx}\tanh x=\frac{1}{\cosh^2x} \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{\cosh^2x}\,dx=\tanh x+C$	(798)
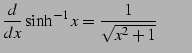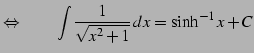$\displaystyle \frac{d}{dx}\sinh^{-1} x=\frac{1}{\sqrt{x^2+1}} \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{\sqrt{x^2+1}}\,dx=\sinh^{-1} x+C$	(799)
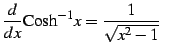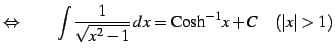$\displaystyle \frac{d}{dx}\mathrm{Cosh}^{-1} x=\frac{1}{\sqrt{x^2-1}} \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{\sqrt{x^2-1}}\,dx=\mathrm{Cosh}^{-1} x+C \quad(\vert x\vert>1)$	(800)
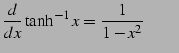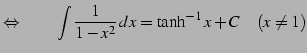$\displaystyle \frac{d}{dx}\tanh^{-1} x=\frac{1}{1-x^2} \qquad$	$\displaystyle \Leftrightarrow\qquad \int\frac{1}{1-x^2}\,dx=\tanh^{-1} x+C \quad(x\neq1)$	(801)

例 5.5 (不定積分の計算例)

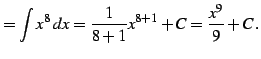$\displaystyle I$	$\displaystyle =\int x^8\,dx= \frac{1}{8+1}x^{8+1}+C= \frac{x^{9}}{9}+C\,.$	(802)
$\displaystyle I$	$\displaystyle =\int\sqrt[4]{x}\,dx= \int x^{\frac{1}{4}}\,dx= \frac{1}{\frac{1}... ...^{\frac{1}{4}+1}+C= \frac{4}{5}x^{\frac{5}{4}}+C= \frac{4\sqrt[4]{x^5}}{5}+C\,.$	(803)
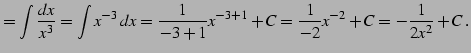$\displaystyle I$	$\displaystyle =\int\frac{dx}{x^3}= \int x^{-3}\,dx= \frac{1}{-3+1}x^{-3+1}+C= \frac{1}{-2}x^{-2}+C= -\frac{1}{2x^2}+C\,.$	(804)
$\displaystyle I$	$\displaystyle =\int(x^3-x^2+3x-2)\,dx= \int x^3\,dx- \int x^2\,dx+ 3\int x\,dx- 2\int dx$	(805)
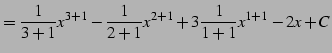	$\displaystyle = \frac{1}{3+1}x^{3+1}- \frac{1}{2+1}x^{2+1}+ 3\frac{1}{1+1}x^{1+1}- 2x+C$	(806)
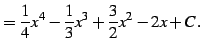	$\displaystyle = \frac{1}{4}x^{4}- \frac{1}{3}x^{3}+ \frac{3}{2}x^{2}- 2x+C\,.$	(807)