Next: 12 テイラー級数を用いた関数の極限の計算 Up: 4 テイラー級数 Previous: 10 項別積分 Contents
11 ランダウの記号
定義 4.43 (ランダウの記号)
関数 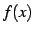 ,
, 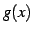 に対して
に対して
が成り立つとき,
と表記する.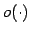 はランダウ(Landau)の記号であり,
「ラージオー」と読む.
またこのとき,
はランダウ(Landau)の記号であり,
「ラージオー」と読む.
またこのとき, 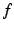 は
は 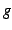 に比べ無視できるという.
に比べ無視できるという.
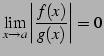 |
(728) |
が成り立つとき,
| (729) |
と表記する.
定義 4.44 (ランダウの記号)
関数 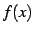 ,
, 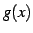 に対して
に対して
が成り立つとき,
と表記する.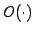 はランダウ(Landau)の記号であり,
「スモールオー」と読む.
またこのとき
はランダウ(Landau)の記号であり,
「スモールオー」と読む.
またこのとき 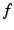 は
は 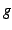 で押さえられるという.
で押さえられるという.
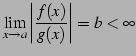 |
(730) |
が成り立つとき,
| (731) |
と表記する.
注意 4.45 (二つのランダウの記号の関係)
関数 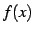 ,
, 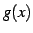 に対して
に対して
が成り立つとき,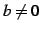 であれば
であれば
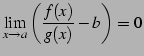 となるので
となるので
が成り立つ.
| (732) |
が成り立つとき,
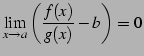 となるので
となるので
| (733) |
が成り立つ.
定義 4.46 (無限大,無限小)
関数 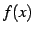 ,
, 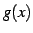 が
が 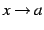 において無限小または
無限大となるとき,次の呼び方を定義する.
において無限小または
無限大となるとき,次の呼び方を定義する.
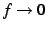 ,
, 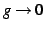 ,
, 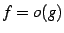
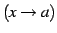 のとき,
のとき,
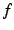 は
は 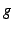 より高次の無限小と呼ぶ.
または
より高次の無限小と呼ぶ.
または 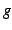 は
は 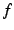 より低次の無限小と呼ぶ.
より低次の無限小と呼ぶ.
-
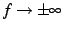 ,
,
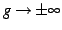 ,
, 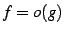
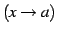 のとき,
のとき,
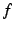 は
は 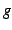 より低次の無限大と呼ぶ.
または
より低次の無限大と呼ぶ.
または 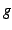 は
は 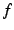 より高次の無限大と呼ぶ.
より高次の無限大と呼ぶ.
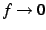 ,
, 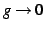 ,
, 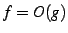
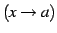 のとき,
のとき,
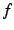 と
と 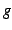 とは同次の無限小と呼ぶ.
とは同次の無限小と呼ぶ.
-
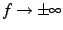 ,
,
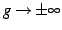 ,
, 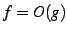
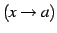 のとき,
のとき,
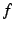 と
と 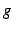 とは同次の無限大と呼ぶ.
とは同次の無限大と呼ぶ.
例 4.47 (ランダウの記号の使用例)
| (734) | ||
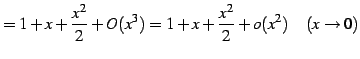 |
(735) |
| (736) | ||
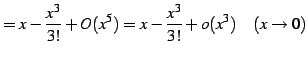 |
(737) |
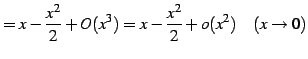 |
(738) | |
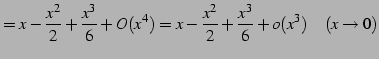 |
(739) |
注意 4.48 (テイラー展開とランダウの記号)
テイラー展開により
が成り立つ.なぜなら
となるからである.同様に
となることより得られる.
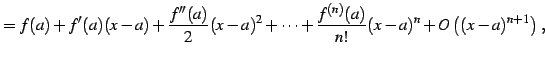 |
(740) | |
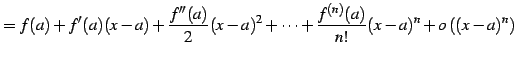 |
(741) |
が成り立つ.なぜなら
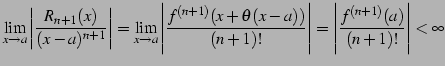 |
(742) |
となるからである.同様に
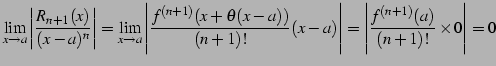 |
(743) |
となることより得られる.
Next: 12 テイラー級数を用いた関数の極限の計算 Up: 4 テイラー級数 Previous: 10 項別積分 Contents
Kondo Koichi
Created at 2003/08/29