Next: 9 項別微分 Up: 4 テイラー級数 Previous: 7 近似関数の誤差の評価 Contents
8 解析関数
定義 4.31 (解析関数)
関数 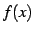 がテイラー級数で表されるとき,
関数
がテイラー級数で表されるとき,
関数 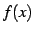 は解析的(analytic)であるという.
解析的な関数を解析関数(analytic function)と呼ぶ.
は解析的(analytic)であるという.
解析的な関数を解析関数(analytic function)と呼ぶ.
定理 4.32 (解析関数の性質)
関数 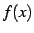 ,
, 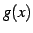 が解析的であるとき,次の関数
が解析的であるとき,次の関数
もまた解析的である.
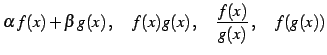 |
(668) |
もまた解析的である.
例 4.33 (テイラー級数の計算例)
関数
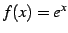 のテイラー級数は
のテイラー級数は
と表わされる. このとき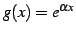 のテイラー級数を求める.
のテイラー級数を求める.
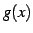 は
は 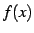 を用いると
を用いると
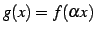 と書ける.
と書ける.
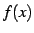 のテイラー級数の
のテイラー級数の 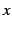 に
に 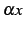 を代入すると
を代入すると
を得る. この展開式はテイラー級数の公式を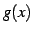 に適用したものと
同じものとなる.
同様に
に適用したものと
同じものとなる.
同様に
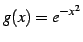 のテイラー級数は
のテイラー級数は
と求まる.
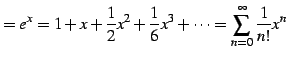 |
(669) |
と表わされる. このとき
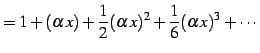 |
(670) | |
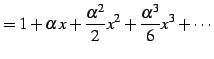 |
(671) |
を得る. この展開式はテイラー級数の公式を
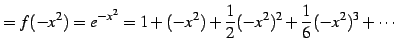 |
(672) | |
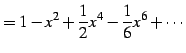 |
(673) | |
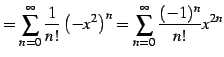 |
(674) |
と求まる.
例 4.34 (テイラー級数の計算例)
| (675) | ||
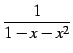 |
(676) | |
| (677) | ||
| (678) |
例 4.35 (テイラー級数の計算例)
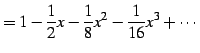 |
(679) | |
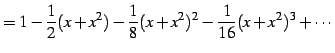 |
(680) | |
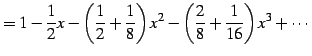 |
(681) | |
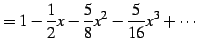 |
(682) |
例 4.36 (テイラー級数の計算例)
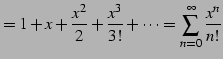 |
(683) | |
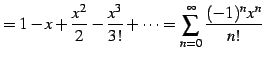 |
(684) | |
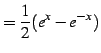 |
(685) | |
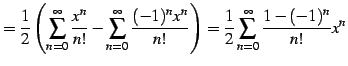 |
(686) | |
| (687) | ||
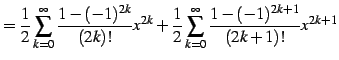 |
(688) | |
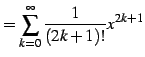 |
(689) | |
| (690) | ||
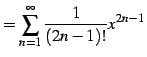 |
(691) |
問 4.37 (テイラー級数の計算)
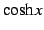 のテイラー級数を求めよ.
のテイラー級数を求めよ.
Next: 9 項別微分 Up: 4 テイラー級数 Previous: 7 近似関数の誤差の評価 Contents
Kondo Koichi
Created at 2003/08/29