Next: 6 テイラー級数による関数の近似 Up: 4 テイラー級数 Previous: 4 テイラー級数の具体例 Contents
5 テイラー展開
テイラー級数では関数 ![]() を無限和で表す.
次のテイラー展開では有限項の和で
を無限和で表す.
次のテイラー展開では有限項の和で ![]() を表す.
を表す.
定理 4.20 (テイラー展開)
関数 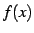 が
が 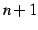 回微分可能なとき,
回微分可能なとき,
が成り立つ. ただし点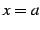 は定義内の点である.
この展開式を
は定義内の点である.
この展開式を 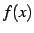 のテイラー展開(Taylor expansion)と呼ぶ.
特に
のテイラー展開(Taylor expansion)と呼ぶ.
特に 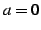 のときを
マクローリン展開(Maclaurin expansion)と呼ぶ.
のときを
マクローリン展開(Maclaurin expansion)と呼ぶ.
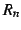 は剰余項(remainder)と呼ばれる.
は剰余項(remainder)と呼ばれる.
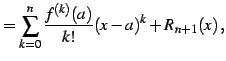 |
(623) | |
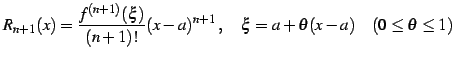 |
(624) |
が成り立つ. ただし点
注意 4.21
点 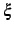 は
点
は
点 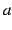 と点
と点 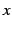 とを
とを
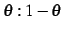 に内分する点である.
に内分する点である.
定理 4.22 (平均値の定理)
関数 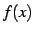 が
が
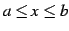 で連続で,
で連続で,
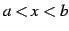 で微分可能ならば,
で微分可能ならば,
を満たす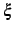 が存在する.
が存在する.
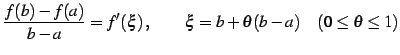 |
(625) |
を満たす
例 4.23 (テイラー展開の具体例)
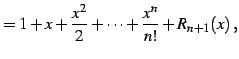 |
(626) | |
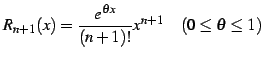 |
(627) |
例 4.24 (テイラー展開の具体例)
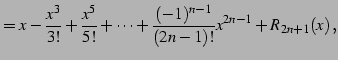 |
(628) | |
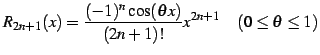 |
(629) |
Kondo Koichi
Created at 2003/08/29